Satellite image and aerial photographs are very important for mapping and creation of spatial data. As well as these aerial photographs and satellite images can be used to create elevation data.
Different methods employed for height measurement for a single given spot/location and also creation of digital elevation model.
Therefore, in this article discuss about displacement in aerial photograph occurred due to relief or height of object on ground.
Relief/Height/Elevation is the most significant source of image displacement. When point/object on the photograph is displaced from its datum position because of its elevation, a displacement take place so this displacement is called Relief displacement or displacement due to height of object.
This relief displacement process can also help to calculate the height of object.
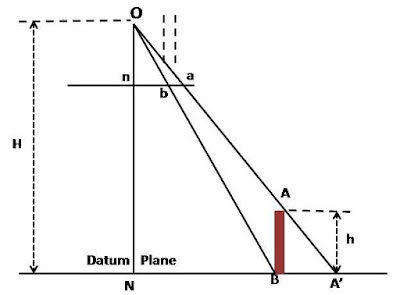
This relief displacement is explained by below figure. In this Figure, ‘O’ is the camera station.
‘NA’ is a flat plain on which stands a tower ‘AB’ with its base at ‘B’. The image of ‘B’ on the truly vertical positive photographic plane is ‘b’.
This is the correct planimetric position (orthogonal) of the image of the tower ‘AB’.
Top ‘A’ is imaged at ‘a’. The image of ‘A’ is thus displaced from its correct planimetric position ‘b’, as ‘A’ is vertically above ‘B’, on the photograph.
This shift of ‘a’ from ‘b’represented by distance ‘ba’ is called relief displacement.
Let ‘h’ be the height of the tower, ‘H’the flying height above the datum plane, ‘n’ and ‘N’ is the photo and ground nadir points (as per the given figure).
na
The scale of photo along na is ————
NA’
ba
The scale of photo along ab is ————
BA’
Since the photograph is truly vertical and datum plane is truly horizontal the scale will be constant.
ba na
Hence ———— = ———-
BA’ NA’
ba BA’
Or ——– = ——– (1)
na NA’
From similar triangles ONA’ and ABA
BA’ h
——– = ——–
NA’ H
Equation (1) becomes
ab h
——– = ——–
na H
h
Hence ab = na* ——–
H
If we denote ‘ab’, the displacement by rd and na, the distance between the nadir point and the image of top of the object by r then we can write the above equation as
h
RD = r ——–
H
From this relation one can conclude :
Relief displacement increases with increasing value of ‘r’ i.e., it is zero at plumb point and maximum at the edges of the photograph.
Smaller the height of the object, smaller is the displacement and vice versa.
If h = o, i.e. for objects in the datum plane there is no displacement.
With increasing value of ‘H’ i.e. with high flying heights the displacement decreases. The satellite pictures can thus be considered having very low relief displacement.
While relief displacement constitutes a source of error in the measurement of horizontal distances on aerial photographs, it is the characteristics that make it possible to study overlapping photographs stereoscopically and in the determination of height differences between objects photographed.
Numerical Example-
Q1. The relief displacement for a tower is 3.01mm and the radial distance from the center of photo to the top of tower is 66.43mm. If the flying height is 1330m above the base of tower, find the height of the tower.
Ans. Here in this question given values are
Relief displacement (RD) = 3.01mm; radial distance (r) = 66.43mm, flying height (H) = 1330m and height of tower (h) need to calculate.
So if use the above formula for relief displacement
h
RD = r ——–
H
First bring all the values to same measurement units- (in this case converted meter to mm)
SO based on that
h
3.01 = 66.43 ———-
1330000
By solving above
h = 60263.43mm
h = 60.26 meters
so height of tower will be 60.26meters
with this method height of object on ground can be calculated using aerial photographs.
I read your blog now share great information here.
wedding photographer nyc